Дать ребенку 1000 примеров и 1000 задач — не лучший способ увлечь его математикой. Детям должно быть интересно, поэтому приходится иногда даже прибегать к волшебству. Например, показывать фокусы. Какие? Рассказывает руководитель проекта «Математические тропинки» Александр Маркеллов.

Чем математические фокусы могут помочь учителям и родителям

• Фокусы всегда помогают наладить контакт с детьми. Первое впечатление самое сильное, особенно у детей. Поэтому во время знакомства я показываю ребятам фокусы - их это завораживает.
• Интересно рассказать новую тему.
• Фокусы не только веселят детей - в каждом из них есть математическая подоплека, поэтому с их помощью можно доступно и интересно объяснить новую тему.

Когда я работал в «Хорошколе», я заметил, что детям сложно понять, что такое переменные и зачем они нужны. Тогда мы предложили ребятам несколько фокусов, которые иллюстрируют эту тему.

1. Фокус с переменными

Загадайте число. Прибавьте к нему 15, затем отнимите 4, потом прибавьте 5, потом отнимите из получившегося числа задуманное. У вас получилось 16.

Как мне удалось угадать ваше число?

Очень просто. И вы даже можете попробовать загадать любое другое число, но результат не изменится. Итак, чтобы понять, что произошло, нам понадобится буквенное выражение. Давайте обозначим задуманное число буквой k, ведь число может быть каким угодно. Если мы запишем все действия буквенным выражением, у нас получится:

k + 15 — 4 + 5 — k

Мы знаем, что 15 — 4 + 5 = 16, значит, мы можем упростить наше выражение. Получается:

k + 16 — k

К задуманному числу мы прибавляем 16, а потом вычитаем задуманное число. Это значит, что наше число исчезает. Теперь очевидно, что мы можем загадать любое число, но в ответе все равно получим 16.

Этот ход оказался удачным — дети остались под впечатлением. Многим из них именно это помогло разобраться в теме. С помощью переменной ребята смогли записать действия с задуманным числом в общем виде и понять механику фокуса.

Наблюдая за реакцией детей на фокусы, я заметил, что существует три уровня понимания: сначала ребенок пробует выполнить фокус, затем — проследить закономерность, и (самое сложное) пытается понять, почему так происходит.

2. Фокус с угадыванием зачеркнутой цифры

Попросите ребенка написать двузначное число, состоящее из разных цифр. Потом предложите поменять цифры местами. Получается два числа; пусть из большего он вычтет меньшее. В результате попросите зачеркнуть любую цифру и назвать оставшуюся. Теперь вы сможете назвать цифру, которую он зачеркнул.

Разбираемся, как узнать зачеркнутую цифру.

Уровень 1. Пробуем выполнить

Например, загаданное число — 37. Меняем цифры местами — получается 73. Вычитаем из большего меньшее: 73 — 37 = 36. Ребенок зачеркивает одну цифру в этом числе и называет мне оставшуюся. Я угадываю цифру, которую он зачеркнул.

Сначала детей действительно поражает, что у них получаются разные ответы, а мне все равно удается угадать цифру.

Уровень 2. Замечаем закономерность

Через какое-то время ребята замечают, что сумма цифр у полученного числа всегда равняется девяти. Например, если у них остается 2, то я вычитаю 2 из 9 и получаю цифру, которую они зачеркнули. Теперь ребята могут повторить этот фокус, но пока не понимают механику.

Иногда ребенок говорит: «Ха, неправильно, я зачеркнул другое число». Это значит, что он неправильно посчитал. Можно предложить ему посчитать вместе.

Уровень 3. Разбираем, как это работает

Механику этого фокуса ребята могут понять начиная с 5-го класса. Давайте попробуем проделать фокус в общем виде.

Двузначное число записывается как «10x + y», то есть у него «x» десятков и «y» единиц. Нам нужно поменять местами цифры. Получается «10y + x».

Теперь вычтем из одного числа другое. Выглядит это так:

«10x + y — 10y — x = 9x — 9y = 9 (x — y)»

Мы видим, что это число делится на 9. Из признаков делимости на 9 мы знаем, что сумма цифр такого числа также будет делиться на 9. Отсюда мы можем сделать вывод, что сумма в ответе будет равна 9.

Кстати, интересную онлайн-вариацию этого фокуса можно найти здесь.

3. Фокус «Удивительная память»

Еще есть классный фокус у Перельмана. Он называется «Удивительная память». Его хорошо показывать детям, с которыми вы уже знакомы, которые знают, что память у вас совершенно обычная.

Раздайте детям такие карточки:

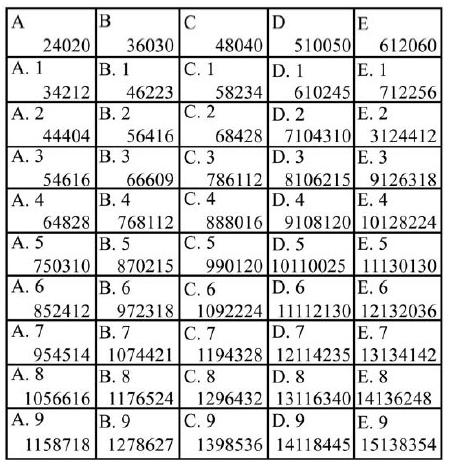
Ребенок называет номер любой ячейки, а вы тут же говорите, какое число там написано. Например, вам говорят: «D5», — и вы мигом отвечаете: «10110025». Числа большие, и их много, поэтому ребята точно удивятся.

Секрет фокуса в том, что значок — буква и цифра — сам указывает на число, которое написано в ячейке.

Прежде всего вы должны помнить, что буква А означает 20, В — 30, С — 40, D — 50, Е — 60.

Поэтому буква вместе с поставленной рядом цифрой означает некоторое число. Например:

А.1 = 21, С. 3 = 43, Е.5 = 65.

Из этого числа вы составляете длинное, написанное на карточке. Как это делается, покажу на примере.

Пусть вам назвали Е.4, т. е. 64.

Во-первых, складываем цифры:

6 + 4= 10.

Во-вторых, умножаем число на 2:

64×2 = 128.

В-третьих, вычитаем из большей цифры меньшую:

6 — 4 = 2.

В-четвертых, перемножаем цифры между собой:

6×4 = 24.

Все результаты пишем рядом. Получаем:

10 128 224.

Это и есть число, написанное на карточке в ячейке Е.4. Кратко произведенные вами выкладки можно обозначить так:

2 — х

То есть умножение, удвоение, вычитание, умножение.

После разбора фокуса можно поговорить с ребятами про кодирование. Наверняка они не знают, что человек, сам не замечая, передает закодированное сообщение.

4. Фокус с монетами

Этот фокус я тоже нашел у Перельмана. Он отлично подходит для изучения четности.

Возьмите в одну руку двухрублевую монету, в другую — пятирублевую. Не показывайте и не говорите мне, где какая монета. Я угадаю это сам. Для этого вам нужно сделать следующее: утройте ту монету, что в правой, и удвойте ту, что в левой. Сложите полученные числа и скажите мне, какая сумма: четная или нечетная. Этого мне достаточно, чтобы безошибочно определить, какая монета зажата у вас в правой руке, а какая — в левой.

Давайте запишем, что происходит, рассматривая четность числа. У нас есть два варианта: в правой руке у вас может быть либо четная монета, либо нечетная.

Разберем первый случай, когда в правой руке у вас находится два рубля. Тогда

(ч х н) + (н х ч)

При умножении четного числа на нечетное мы получаем четное число, значит

ч + ч = ч

В этом случае у нас получается четное число.

Теперь посмотрим на другой случай, когда в правой руке у нас монета номиналом 5 рублей.

Тогда:

(н х н) + (ч х ч) = н + ч = н

В этом случае мы всегда будем получать нечетное число.

Используйте эти нехитрые фокусы в обучении. Ребята поймут, что математика — интересная и полезная наука, и будут ждать ваших занятий с нетерпением.